Pogledajte samo ovaj broj: 6174.

Na prvi pogled, ne djeluje posebno – ali on intrigira matematičare i zaluđenike za brojeve još od 1949. godine.
Zašto? Uzmite ove fascinantne činjenice i uvjerite se sami:
- Izaberite četvorocifreni broj, bilo koji broj, sa najmanje dvije različite cifre (uključujući nulu). Na primer, 1234
- Rasporedite cifre od najveće ka najmanjoj: 4321
- Sad ih složite od najmanje ka najvećoj: 1234
- Oduzmite manji broj od većeg: 4321 – 1234
- Sad ponovite korake 2, 3 i 4 sa brojem koji ste dobili
Uradimo to zajedno
- 4321 – 1234 = 3087
- Rasporedite cifre od najveće ka najmanjoj: 8730
- Složite ih od najmanje ka najvećoj: 0378
- Oduzmite manji broj od većeg: 8730 – 0378 = 8352
- Ponovimo prethodna tri koraka sa brojem koji smo dobili
Sad, dakle, radimo sa 8352
- 8532 – 2358 =6174
I ponovimo to sa 6174 – složivši njegove cifre od najveće ka najmanjoj i od najmanje ka najvećoj i izvršimo oduzimanje dva dobijena broja
- 7641 – 1467 = 6174
Kao što vidite, od ovog koraka nadalje ne vrijedi više nastavljati s ovim – uvijek ćete dobiti istu operaciju i isti rezultat: 6174
U redu, možda ćete pomislite da je to samo slučajnost. Ajde onda da probamo to sa nekim drugim nasumičnim brojem. Šta kažete na 2005?
- 5200 – 0025 = 5175
- 7551 – 1557 = 5994
- 9954 – 4599 = 5355
- 5553 – 3555 = 1998
- 9981 – 1899 = 8082
- 8820 – 0288 = 8532
- 8532 – 2358 = 6174
- 7641 – 1467 = 6174
Ispostavlja se da bilo koji četvorocifreni broj da odaberete, prije ili kasnije stići ćete do 6174, a od tad pa nadalje operacija je uvijek ista, s istim rezultatom.
Kaprekarova konstanta
Čestitamo, upoznali ste se sa Kaprekarovom konstantom.

Indijski matematičar Datatreja Ramčandra Kaprekar (1905-1986) volio je da se igra s brojkama i tako je nabasao na misterioznu ljepotu broja 6174.
D.R. Kaprekar – po vlastitom priznanju zavisnik od teorije brojeva – predstavio je svoje otkriće svijetu na matematičkoj konferenciji održanoj u indijskom gradu Madrasu 1949. godine.
„Pijanica želi da nastavi da pije vino kako bi neprestano bio u tom prijatnom stanju. Ista stvar važi za mene kad su u pitanju brojevi”, imao je običaj da kaže.
Kaprekar se školovao na Univerzitetu u Mumbaju i život proveo kao školski nastavnik u malom indijskom gradu Devlali, u brdima sjeverno od Mumbaja.
Iako je njegovo otkriće naišlo na podsmijeh i otpisivanje među indijskim matematičarima – za koje je njegov rad bio trivijalan i irelevantan – bio je produktivan autor, uglavnom u publikacijama o popularnoj nauci.
Često je bio pozivan i da učestvuje na konferencijama ili da govori u školama i na fakultetima o svojim neobičnim metodama i fascinantnim opservacijama o brojevima.
Ko se poslednji smije…

Postepeno, Kaprekarove ideje su počele da uzimaju maha kod kuće i u inostranstvu – sedamdesetih godina američki autor bestselera i zaluđenik za matematiku Martin Gardner pisao je o njemu u časopisu za popularnu nauku Sajentifik Amerika (Scientific America).
Danas su Kaprekar i njegova otkrića priznati i proučavani među matematičarima širom svijeta, naročito onim koji – poput njega – ne mogu da odole igranju sa brojevima.
Jutaka Nišijama, profesor na Univerzitetu ekonomije u Osaki, kaže: „Broj 6174 je zaista misteriozan broj”.
U članku objavljenom u onlajn magazinu +plus, Nišijama objašnjava kako se „poslužio kompjuterom da provjeri da li svi četvorocifreni brojevi na kraju udare u zid u vidu broja 6174 u ograničenom broju koraka.”
Njegovo otkriće? Svi četvorocifreni brojevi, kod kojih sve cifre nisu iste, stignu do 6174 po Kaprakarovom metodu u najviše sedam koraka.
„Ako ne stignete do 6174 koristeći Kaprekarovu operaciju sedam puta, onda ste napravili grešku u računici i treba da probate ponovo!”, kaže Nišijama.
Magični brojevi
U slučaju da se pitate koliko drugih „specijalnih brojeva” postoji… odgovor je… ne znamo tačno.
Ali ono što znamo jeste da postoji sličan fenomen Kaprekarovoj konstanti za trocifrene brojeve.
Otkrijmo ga. Mogli bismo da krenemo sa bilo kojim nasumičnim trocifrenim brojem, kao što je 574:
- 754 – 457 = 297
- 972 – 279 = 693
- 963 – 369 = 594
- 954 – 459 = 495
- 954 – 459 = 495
I eto ga: „magični broj” je 495.
Matematičari kažu da se ove konstante dešavaju samo sa trocifrenim i četvorocifrenim brojevima, ali su se oni do sada igrali samo s onima između dvocifrenih i desetocifrenih.
6174, u tehnikoloru

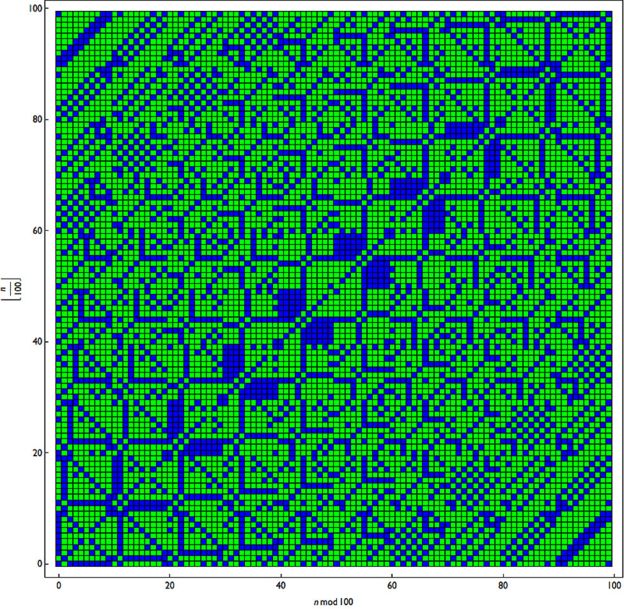
Fondacija Scigram tehnolodžiz je indijska kompanija smještena na jugu Mumbaja i razvija „platformu IT učenja” za ruralne i plemenske škole. Odlučila je da uzme broj 6174 i poigra se s ciframa i bojama.
Osnivač Giriš Arabale rekao je za BBC da je oduvjek bio zainteresovan za motivisanje školske djece – naročite one koja mrzi matematiku – i želeo je da im pokaže da i tu ima zabave.
„Kaprekarova konstanta je jedna velika ljepotica”, kaže Arabale. „Kad slijedite korake, dovedu vas do predivnog ‘Aha! momenta’. Tako nešto se ne dešava baš često kad učite iz tradicionalnog školskog programa za matematiku.”
Sa tim na umu, Arabaleov tim odlučio je da kodira bojama korake neophodne da se stigne do 6174- uzimajući u obzir da ne treba nikad više od sedam operacija da se stigne do „magičnog” broja.
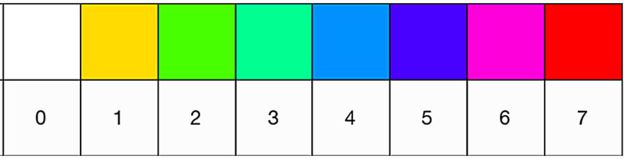
To je postala osnova za kod koji lako može da se rekonstruiše na Raspberi piu – jeftinom kompjuteru veličine kreditne kartice koji je popularna alatka u učenjima STEM-a (Nauka, tehnologija, inženjerstvo i matematika).
Potom studenti mogu da ga protumače koristeći jezik Volfram (opšti multi-paradigmatski kompjuterski jezik, dostupan besplatno na Raspberi piu) i upotrebe program na svakom od postojećih 10.000 četvorocifenih brojeva.
To stvara obrazac sa brojem koraka neophodnim da se stigne do 6174 i slaže ih na višebojnu koordinatnu mrežu.
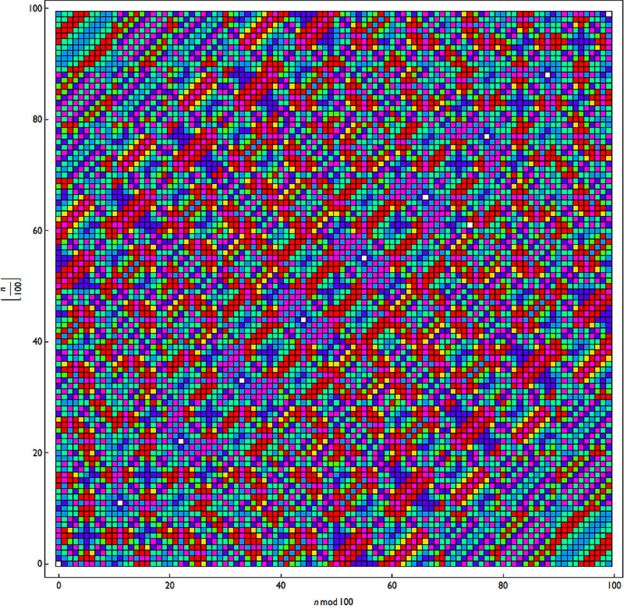
Jednom kad počnete da kodirate… šta biste vidjeli kad biste neparne brojeve predstavili plavom a parne brojeve zelenom?
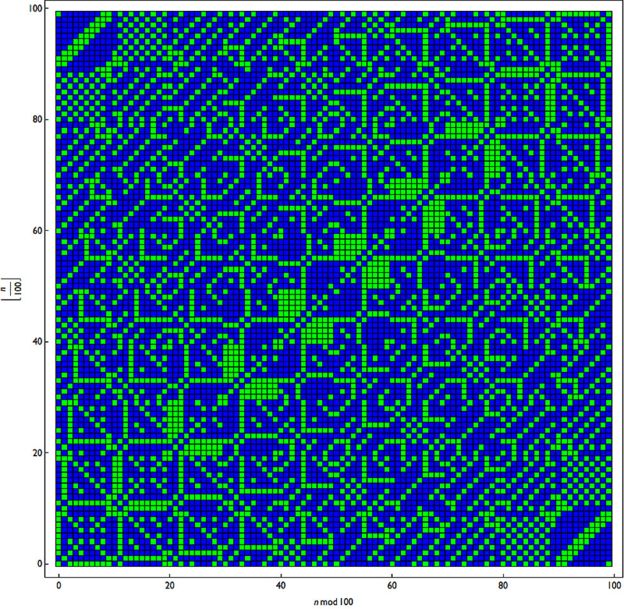
A ako predstavite proste brojeve zelenom a ostale plavom? Da li se obrazac mijenja u značajnijoj mjeri?
Rekreativna matematika

Kaprekarova konstanta nije bila njegov jedini doprinos rekreativnoj matematici, koja igranje sa brojevima doživljava kao najbolji oblik zabave.
Možda ste čuli i za Kaprekarov broj: pozitivni broj sa odlikom da, kad se kvadrira, njegov rezultat može da se razdvoji u dva pozitivna broja čiji je zbir uvijek jednak prvobitnom broju.
Možda će vam biti jasnije ovdje na primjeru:
- 297² = 88,209
- 88 + 209 = 297
Drugi dobri primjeri Kaprekarovih brojeva su: 9, 45, 55, 99, 703, 999, 2,223, 17,344, 538,461… Isprobajte ih sami i vidite šta će se desiti!
Zapamtite: kad saberete brojeve koje dobijete, razdvojte broj cifara ravnopravno kad god je to moguće: jednocifreni broj plus jednocifreni broj; dvocifreni broj plus dvocifreni broj…
Ali ako broj koji dobijete kvadriranjem ne može da se razdvoji na dvije brojke s istim brojem cifara, kao u primjeru iznad (88.209 ima pet cifara), podijelite ga tako da dobijete jedan dvocifreni i jedan trocifreni broj (88+209).
I, uzgred, dok to radite, možda biste voljeli da znate da se to što radite zove Kaprekarova operacija.